Cópulas: su concepto y utilidad en la medición de riesgos
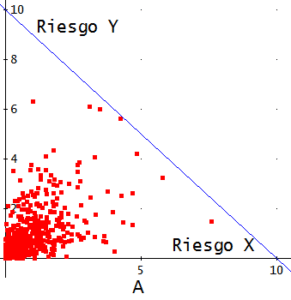
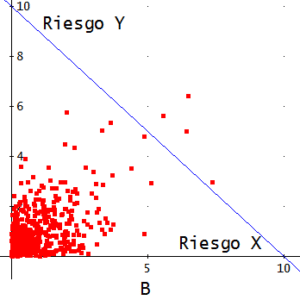
Los riesgos X e Y han sido simulados a partir de la misma función de distribución y tienen, por tanto, la misma media, varianza, etc. Pero ambos gráficos, A y B, difieren en algo muy importante: en A no hay ningún caso en que la suma del importe del riesgo X más el importe del Y superen 10 unidades, mientras que en el B son varios los resultados que sí superan ese umbral (representado, en A y en B, por la línea recta que desciende en diagonal). ¿Se debe esta diferencia a que el coeficiente de correlación es mayor en B que en A? No. En ambos casos dicho coeficiente es 0,5. La mayor peligrosidad del conjunto de riesgos (X,Y) en el gráfico B proviene de la distinta manera en que dependen estos riesgos entre sí, que no capta el coeficiente de correlación.
El ejemplo examinado nos lleva a la conclusión de que en cualquier función de distribución bivariante (y, en general, multivariante) quedan regulados los dos aspectos que definen el comportamiento estadístico de sus variables:
- La distribución marginal de cada una, es decir, cómo se comporta estadísticamente cuando la observamos de forma aislada de la otra variable.
- El comportamiento conjunto de ambas variables o estructura de dependencia. La cópula es la función (en nuestro ejemplo, de dos variables) que regula dicho comportamiento conjunto y sólo él, es decir, nada nos dice la cópula sobre el comportamiento marginal de dichas variables.
Para obtener la cópula a partir de la función de distribución hemos de «extraer» de la misma las distribuciones marginales. Lo que queda tras esta operación, es la cópula. Si tenemos una función de distribución de dos variables F(x,y) con funciones de distribución marginal u=g(x), v=h(y) sabemos que estas funciones g y h están determinando la forma de la función F(x,y) de manera que para «aislar» o dejar sola a la función cópula hemos de «deshacer» el efecto que g y h ejercen en F(x,y). Ello puede hacerse en dos pasos:
Primero, obtener las funciones inversas g-1 y h-1, lo que hacemos despejando en ellas x e y, respectivamente. Obtenemos así x= g-1(u), y= h-1(v). Observemos que u y v representan la probabilidad que corresponde a cada valor de x e y según la función de distribución marginal g y h, es decir que u y v oscilan entre 0 y 1.
Segundo, insertar en F(x,y) las expresiones que acabamos de obtener, x= g-1(u), y= h-1(v). Con ello resulta que F(x, y) = F[g-1(u), h-1(v)] es decir, en definitiva, una función que depende de u y v que suele designarse por C(u,v) y a la que llamamos cópula.
La cópula es, por tanto, «lo que queda» de una función de distribución al eliminar de la misma el comportamiento marginal de las variables y que necesariamente es lo que regula y determina la estructura de dependencia entre esas variables. Es una función definida para valores comprendidos entre 0 y 1 de sus variables independientes. En realidad es la función de distribución conjunta de las variables uniformes (0,1). En la siguiente gráfica se representa la función de densidad de la cópula correspondiente a una distribución t de Student con 4 grados de libertad y coeficiente de correlación 0,6.
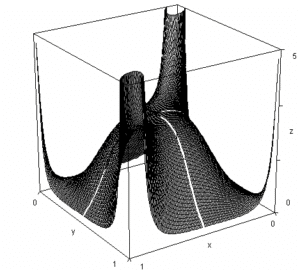
Hemos obtenido la cópula a partir de una función de distribución. Pues bien, cabe igualmente seguir el camino inverso: A partir de la cópula, llegar a la función de distribución sin más que «conectar» a aquélla las funciones de distribución marginal. Es decir, que simbólicamente tendríamos:
Cópula + Distribuciones marginales = Función de distribución conjunta
Y también:
Función de distribución conjunta – Distribuciones marginales = Cópula
La posibilidad de combinar un determinado modelo de cópula con distintas funciones de distribución y, análogamente, un cierto conjunto de éstas con diversos modelos de cópula, abre una multiplicidad de modelos diferentes para describir el comportamiento estadístico conjunto de dos o más variables aleatorias (es decir, de modelos de distribución conjunta).
Hemos visto cómo puede obtenerse una cópula desde una distribución multinomial conocida (Gauss, t de Student). Pero pueden obtenerse también distintos modelos de cópula si elaboramos funciones que reúnan los requisitos esenciales para que el resultado sea una cópula. Y así, además de las cópulas ya citadas de Gauss y de Student, existen otras muchas como la de Clayton, de Gumbel, de Frank, etcétera, de manera que el profesional dispone de una variedad notable para modelizar el fenómeno que interese.
¿Qué utilidad tienen las cópulas? Allá donde exista una diversidad de riesgos que puedan presentar dependencia entre sí, habrá campo para intentar la aplicación de las cópulas. Las normativas de las entidades financieras (bancos y aseguradoras) tienden a incluir en los sistemas de solvencia una pluralidad de riesgos que les afectan. De estos riesgos no interesa sólo cómo se distribuyen aislada o separadamente (distribución marginal) sino también de qué manera dependen los unos de los otros. Puede ocurrir que en condiciones normales no exista dependencia entre ellos, pero cuando haya crisis las cosas empeoren en todos ellos. Ésta es una situación en que el coeficiente de correlación no es instrumento adecuado, mientras que la aplicación de la teoría de cópulas puede ofrecer respuesta satisfactoria. En la normativa de la Unión Europea sobre solvencia de entidades aseguradoras (Solvencia II) se sale del paso aumentando el coeficiente de correlación en grado que se estima suficiente para cubrir esa mayor dependencia que puede darse en situaciones críticas. Aun con la ventaja de su simplicidad, esta solución nos parece demasiado tosca para ser satisfactoria. De ahí que sea aconsejable, en casos así, considerar la aplicación de dicha Teoría de cópulas, que puede ofrecer modelos lo suficientemente flexibles para adaptarse a gran variedad de fenómenos.
El lector interesado puede utilizar mi trabajo titulado Teoría de Cópulas. Introducción y Aplicaciones a Solvencia II (Fundación MAPFRE) como una introducción a este tema y continuar después con el estudio de la extensa bibliografía disponible sobre él, prueba del gran interés que está mereciendo entre los estudiosos y profesionales de estas cuestiones.




